PROBLEM DESCRIPTION
You are given n balloons, indexed from 0 to n - 1. Each balloon is painted with a number on it represented by an array nums. You are asked to burst all the balloons.
If you burst the ith balloon, you will get nums[i - 1] nums[i] nums[i + 1] coins. If i - 1 or i + 1 goes out of bounds of the array, then treat it as if there is a balloon with a 1 painted on it.
Return the maximum coins you can collect by bursting the balloons wisely.
SOLUTION
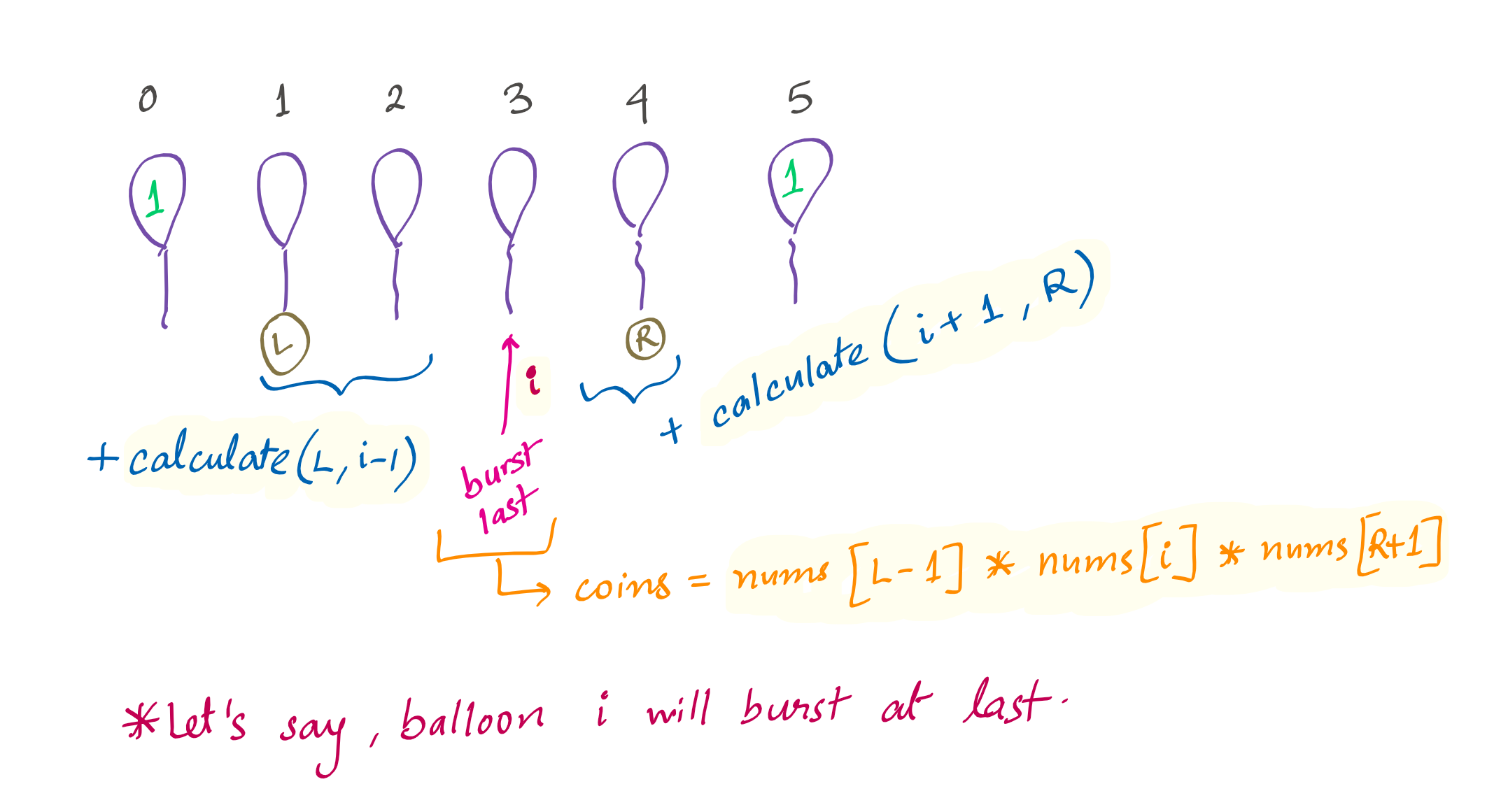
The following solution which uses HashMap to cache the intermediate answers will timeout. Use 2D matrix to optimize.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
public int maxCoins(int[] nums) {
int[] numsModified = new int[nums.length+2];
numsModified[0] = 1;
numsModified[numsModified.length-1] = 1;
for(int i=0; i<nums.length; i++){
numsModified[i+1] = nums[i];
}
return coinsHelper(numsModified, 1, numsModified.length-2, new HashMap<String, Integer>());
}
public int coinsHelper(int[] nums, int l, int r, Map<String, Integer> map){
if(l > r) return 0;
if(!map.containsKey(l+":"+r)){
int maxCoins = 0;
for(int i=l; i<=r; i++){
int coins = coinsHelper(nums, l, i-1, map) +
nums[l-1] * nums[i] * nums[r+1] +
coinsHelper(nums, i+1, r, map);
maxCoins = Math.max(maxCoins, coins);
}
map.put(l+":"+r, maxCoins);
}
return map.get(l+":"+r);
}
}
OPTIMIZATION
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
class Solution {
public int maxCoins(int[] nums) {
int[] numsModified = new int[nums.length+2];
//include element 1 at the beginning and at the end for easier calculation
numsModified[0] = 1;
numsModified[numsModified.length-1] = 1;
//copy the original array to modified array
for(int i=0; i<nums.length; i++){
numsModified[i+1] = nums[i];
}
//init dp array
int[][] dp = new int[numsModified.length-1][numsModified.length-1];
for(int i=0; i<dp.length; i++) Arrays.fill(dp[i], -1);
//we have modified the original array by adding 1 to front and back, so we need to take Left as 1 and Right as length-2 in the modifed array
return coinsHelper(numsModified, 1, numsModified.length-2, dp);
}
public int coinsHelper(int[] nums, int l, int r, int[][] dp){
//base case
if(l > r) return 0;
if(dp[l][r] == -1){
int maxCoins = 0;
//IMPORTANT: for each balloon, we calculate coins considering that it will bursted LAST.
for(int i=l; i<=r; i++){
int coins = coinsHelper(nums, l, i-1, dp) + //for left subarray before index i
nums[l-1] * nums[i] * nums[r+1] + //coins when we burst current balloon
coinsHelper(nums, i+1, r, dp); //for right subarray after index i
//update max
maxCoins = Math.max(maxCoins, coins);
}
dp[l][r] = maxCoins;
}
return dp[l][r];
}
}
