Largest BST (geeksforgeeks - SDE Sheet)

class Solution{

    static int MIN = 0;
    static int MAX = 1000001;

    // return the size of the largest sub-tree which is also a BST
    static int largestBst(Node root)
    {
        if(root == null)
            return 0;

        // if root is already a valid BST, then we don't need to check its sub trees since they cannot has larger size
        if(isBST(root, MIN, MAX))
            return size(root);

        return Math.max(largestBst(root.left), largestBst(root.right));
    }

    // get the number of nodes in the current binary tree
    static public int size(Node root){

        if(root == null)
            return 0;

        int lst = size(root.left);
        int rst = size(root.right);

        return 1 + lst + rst;

    }

    // check if the current binary tree is a valid BST
    static public boolean isBST(Node root, int minVal, int maxVal){

        if(root == null)
            return true;

        // as per the example, duplicates should go to left tree
        if(root.data < minVal || root.data >= maxVal)
            return false;

        // since duplicates are allowed and they need to go to left tree
        // we set the maxValue on left to be the same as current root value
        boolean lst = isBST(root.left, minVal, root.data);
        boolean rst = isBST(root.right, root.data+1, maxVal);

        return lst && rst;
    }

}

class Solution{

    static int MIN = Integer.MIN_VALUE;
    static int MAX = Integer.MAX_VALUE;

    static int largestBst(Node root)
    {
        return largestBstHelper(root).maxSize;
    }

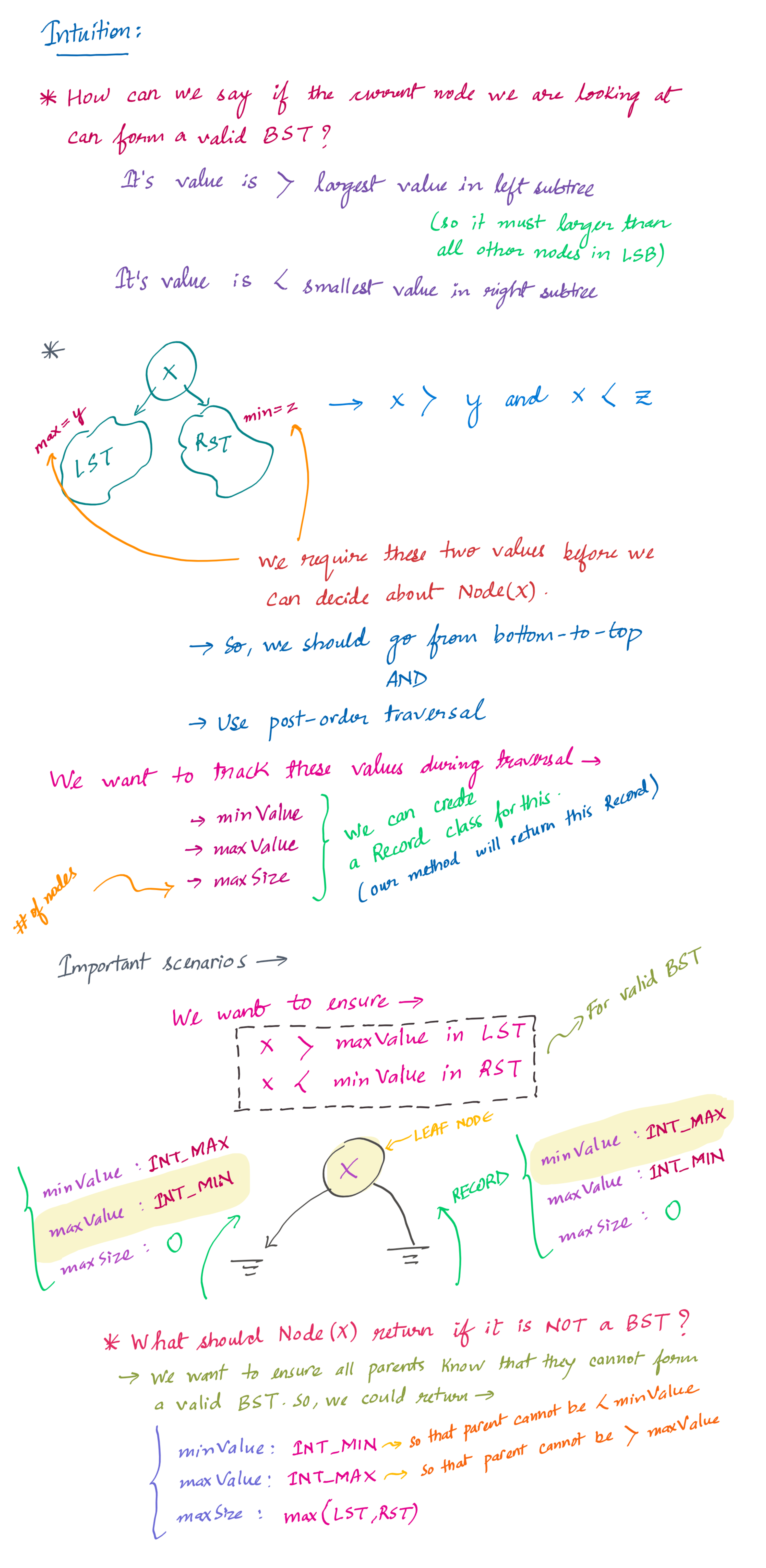
    static Record largestBstHelper(Node root){

        // root == null is actually a valid BST with size 0
        // we want its parent (if there is any) to take this as a valid BST when comparing
        // Let's say the value of parent node is X
        // so, we want: x > maxValue in LST and x < minValue in RST
        // If we set maxValue to be INT_MIN, and minValue to be INT_MAX, the above should be true
        if(root == null){
            return new Record(MAX, MIN, 0);
        }

        // post-order
        // why?
        // we will need the values of min and max from both LST and RST before evaluating the current node
        Record left = largestBstHelper(root.left);
        Record right = largestBstHelper(root.right);

        // validate the tree formed using current node
        // if the value at current node is more than the largest value on left sub tree
        // and
        // if the value at current node is less than the smallest value on the right sub tree
        // then the current node must be forming a valid BST

        if(root.data > left.maxValue && root.data < right.minValue){
            return new Record(Math.min(root.data, left.minValue), Math.max(root.data, right.maxValue), 1 + left.maxSize + right.maxSize);
        }

        // it's not a BST
        return new Record(MIN, MAX, Math.max(left.maxSize, right.maxSize));

    }

}

class Record{

    int minValue;
    int maxValue;
    int maxSize;

    Record(){}

    Record(int minValue, int maxValue, int maxSize){
        this.minValue = minValue;
        this.maxValue = maxValue;
        this.maxSize = maxSize;
    }

}