PROBLEM DESCRIPTION
There are some spherical balloons taped onto a flat wall that represents the XY-plane. The balloons are represented as a 2D integer array points where points[i] = [xstart, xend] denotes a balloon whose horizontal diameter stretches between xstart and xend. You do not know the exact y-coordinates of the balloons.
Arrows can be shot up directly vertically (in the positive y-direction) from different points along the x-axis. A balloon with xstart and xend is burst by an arrow shot at x if xstart <= x <= xend. There is no limit to the number of arrows that can be shot. A shot arrow keeps traveling up infinitely, bursting any balloons in its path.
Given the array points, return the minimum number of arrows that must be shot to burst all balloons.
SOLUTION
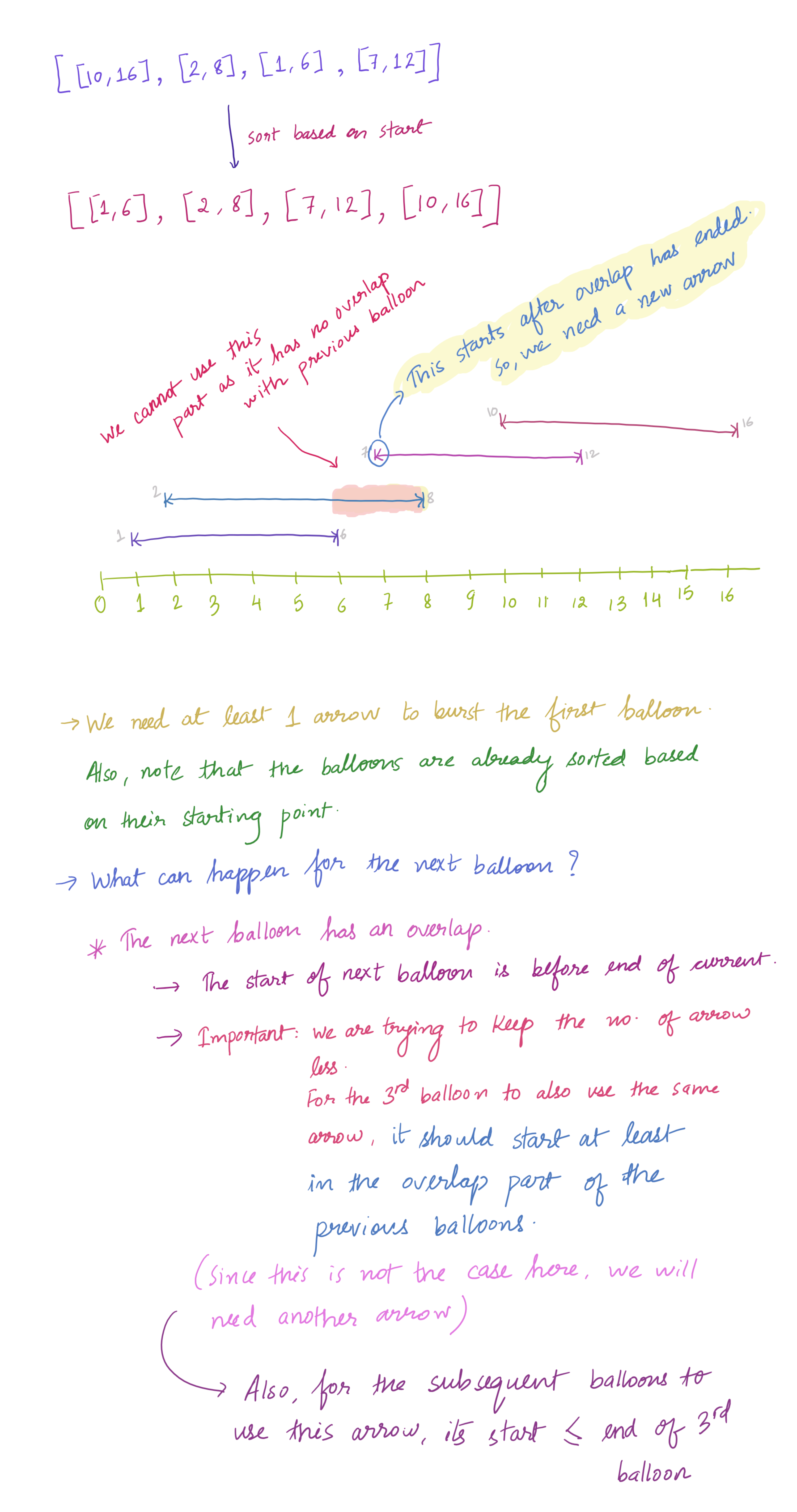
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public int findMinArrowShots(int[][] points) {
int n = points.length;
// Sort the points based on their starting x-coordinate.
Arrays.sort(points, (o1, o2) -> o1[0] > o2[0] ? 1 : (o1[0] < o2[0] ? -1 : 0));
// Initialize the number of arrows needed to 1 (assuming there's at least one balloon).
int count = 1;
// Initialize the end position of the first balloon.
int end = points[0][1];
for (int i = 1; i < n; i++) {
// If the current balloon overlaps with the previous one, no need to increase count
// But, update the end position to MIN(previousEnd, currentEnd)
// To use the same arrow, we would need to shoot in the common area which will be bounded by min end co-ordinate
if (points[i][0] <= end) {
end = Math.min(end, points[i][1]);
} else {
// If there's no overlap, increment the arrow count and set a new end position.
count++;
end = points[i][1]; //note: this is no longer related to previous end
}
}
return count;
}
}
