Problem Description
Given an array of positive and negative numbers, find if there is a subarray (of size at-least one) with 0 sum.
Subarray with 0 sum
Solution
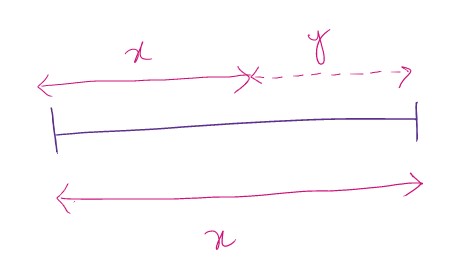
If the sum of elements for a given range is x. And there exists another range x as shown in the above diagram which sum x. That means that the sum of elements in the y region must be 0.
So, we can first create a Prefix Sum Array of the given array. If there exists two elements in the prefix sum with the same value, that means the sum of elements between them must be 0.
The trivial case if when the prefix sum itself is 0. [The below code can be further optimized to return true while we are constructing the prefix array. Also, rather than getting the frequency of all elements in prefix array first, we can keep adding elements one by one in the HashMap and check if that already exists.]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution{
//Function to check whether there is a subarray present with 0-sum or not.
static boolean findsum(int arr[],int n)
{
//Your code here
int pf[] = new int[n];
pf[0] = arr[0];
for(int i=1;i<n;i++){
pf[i] = pf[i-1] + arr[i];
}
boolean out=false;
Map<Integer, Integer> map = new HashMap<>();
for(int i=0; i<n; i++){
if(pf[i] == 0){
return true;
}
Integer frequency = map.get(pf[i]);
if(frequency == null){
map.put(pf[i],1);
}else{
map.put(pf[i],1+frequency);
}
}
for(Map.Entry<Integer,Integer> entry : map.entrySet()){
if(entry.getValue() > 1){
return true;
}
}
return out;
}
}
