Problem Description
Return the total sum of all sub-arrays of the given array.
Solution
BRUTE-FORCE
The brute force method is to check all sub-array, calculate its sum and add that to the total sum.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public static int totalSumSubArrayBruteForce(ArrayList<Integer> A) {
int totalSum = 0;
for(int i=0; i<A.size(); i++) {
int currentSum=0;
for(int j=i; j<A.size(); j++) {
//We will optimize this loop next.
for(int k=i; k<=j; k++) {
currentSum+=A.get(k);
}
}
totalSum+=currentSum;
}
return totalSum;
}
OPTIMIZATION – 1 (Prefix Sum)
In the previous code, we use an inner nested loop to calculate the sum of elements from a given start and end index. We can optimize this to O(1) time complexity and O(N) space complexity by using a prefix array sum.
The overall time-complexity to find the sum of all subarray will still remain O(N^2).
1
2
3
for(int k=i; k<=j; k++) {
currentSum+=A.get(k);
}
Use:
1
2
3
4
5
6
public getSum(int L, int R, int[] pf){
if(L == 0)
return pf[R];
else
return pf[R] - pf[L-1];
}
OPTIMIZATION – 2 (Carry Forward)
The calculation of sum from a given start and end index can further be improved to O(1) space comlexity by using carry forward technique.
The overall time-complexity to find the sum of all subarray will still remain O(N^2).
1
2
3
4
5
6
7
for(s=0; s<n; s++){
currentSum=0;
for(i=s; i<n; i++){
currentSum = currentSum + A[i]; //carry forward
totalSum += currentSum;
}
}
OPTIMIZATION – 3 (Contributaion Method) – O(N) Time Complexity
We can optimize it to O(N) with a few observations:
[1, 2, 3, 4]
0 1 2 3
Let’s say, we need to find out “How many sub-arrays are there, which contain the index “2”.
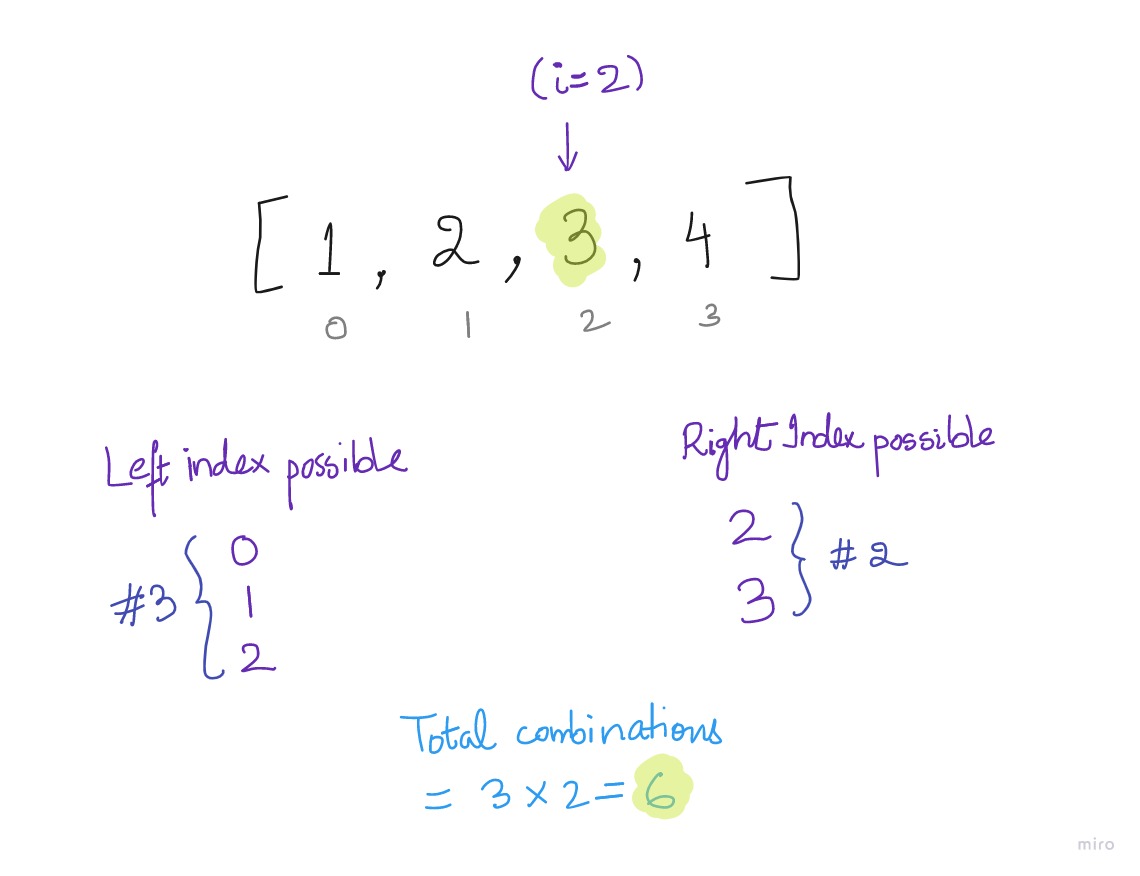
We can say that the sub-array which contains index 2, must have a starting index in (0, 1, 2). Note that we are including 2 since [2] itself will also be considered as a sub-array with single element.
Similarly, we can say that the sub-array which contains index 2 must have an end index in (2, 3).
So, total number of sub-arrays which contains index 2 are:
3 x 2 = 6 (number of indices on left multiplied by number of indices on the right)
We can now say that, index 2, which has the element 3 is present in 6 sub-arrays
This observation is very important because now, we know that the contributation of index 2 (element 3) to the total sum of all sub-arrays is: 3 x 6 = 18.
In general, the number of sub-arrays possible for any index i will be:
(i+1) x (N-i) where N is the length of the array
Using this approach, we can calculate the total number of sub-arrays containing index 0,1,2…(n-1).
The contribution to total sum by each element will be: (element at i index) X (number of sub-arrays containing index i). And the total sum of all sub-arrays will be the total sum of all the previous resulsts, which is the contribution of each element to the total sum.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
package com.test;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class Solution {
public static void main(String[] args) {
List<Integer> list = Arrays.asList(1, 2, 3, 4);
ArrayList<Integer> l = new ArrayList<>(list);
System.out.println(totalSumSubArray(l));
System.out.println(totalSumSubArrayBruteForce(l));
}
public static int totalSumSubArrayBruteForce(ArrayList<Integer> A) {
int totalSum = 0;
for(int i=0; i<A.size(); i++) {
int currentSum=0;
for(int j=i; j<A.size(); j++) {
for(int k=i; k<=j; k++) {
currentSum+=A.get(k);
}
}
totalSum+=currentSum;
}
return totalSum;
}
public static int totalSumSubArray(ArrayList<Integer> A) {
int totalSum = 0;
for(int i=0; i<A.size(); i++) {
totalSum += solve(A, i) * A.get(i);
}
return totalSum;
}
//Given a list, how many subarrays have the given index present in it?
public static int solve(ArrayList<Integer> A, int index) {
//The starting index can be: [0,1,2,3...index]
//The end index can be: [index, index+1, index+1...n-1]
//So, the total possible subarrays will be, total combinations possible for the above values
int start = index+1;
int end = A.size()-index;
return start*end;
}
}
