PROBLEM DESCRIPTION
You are given an array of integers A of size N. The value of a subarray is defined as BITWISE OR of all elements in it. Return the sum of value of all subarrays of A % 109 + 7.
SOLUTION
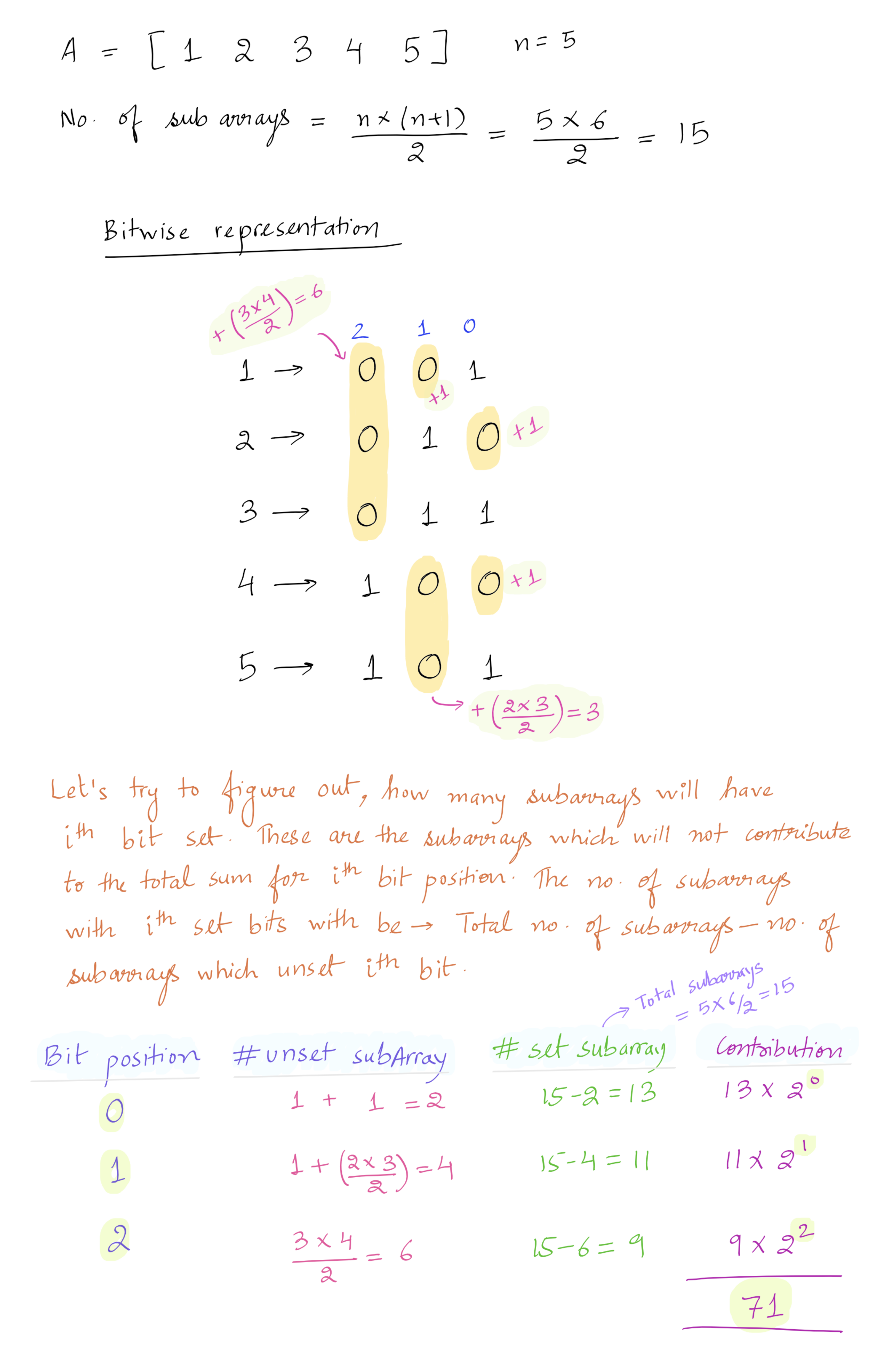
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
public class Solution {
long M = 1000000007;
public int solve(int[] A) {
int n = A.length;
//total number of sub arrays possible
long totalSubarrays = sumOfN(n); // n*n+1/2
//init: total sum (answer)
long total = 0;
//for each bit position
for(int i=0; i<=31; i++){
//get the number of subarrays which have ith bit as unset
long subArrayUnsetBit = calcSubArrayUnsetBitAtPos(i, A, n);
//number of sub arrays which have ith bit set
long subArraySetBit = totalSubarrays - subArrayUnsetBit;
//if ith bit is set, its value would be: 2^i == (1<<i)
long powerValue = (1<<i);
//contribution to total sum by all subarrays which has set bit at ith position
long contribution = (subArraySetBit * powerValue);
total = (total + contribution);
}
return (int)(total%M);
}
//Calculate the number of sub arrays with unset ith bit position
public long calcSubArrayUnsetBitAtPos(int position, int[] A, int n){
//init:
long total = 0;
long current = 0;
//for each element, check if bit at "position" is unset
//if it's unset, add to the total
//since we are looking for number of subarrays, if there are continuous unset bit position, the number of subarrays will depend on it as well. See the explanation in the image
for(int i=0; i<n; i++){
if(!checkSetAtPosition(position, A[i])){
current++;
}else {
total = total + sumOfN(current);
current = 0; //reset
}
}
total = total + sumOfN(current);
return total;
}
//check if the ith bit is set in N
public boolean checkSetAtPosition(int i, int n){
if( (n&(1<<i)) != 0){
return true;
}else
return false;
}
//sum of first N natural numbers
public long sumOfN(long n){
return (n*(n+1))/2;
}
}
